滨州天气40天预报_30天天气预报最准确滨州市

1.七年级数学正数和负数教案

2.为什么天老是闷热还不下雨，但天气预报的有雨啊？

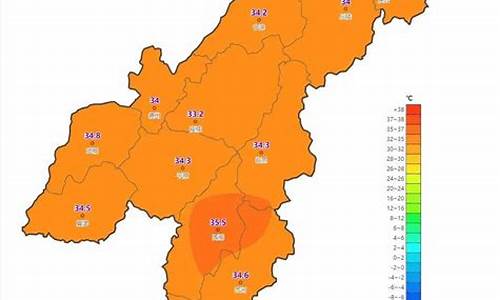
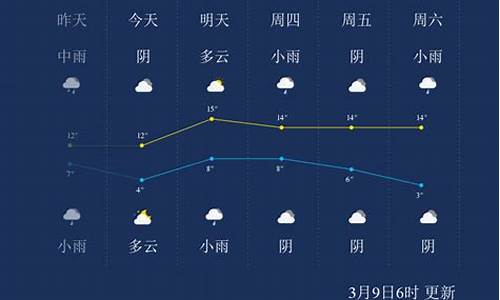
1日星期日 晴 高温 3℃ 无持续风向 微风

2日星期一 多云 高温 2℃ 北风 3-4级

3日星期二 多云 高温 -2℃ 北风 3-4级

4日星期三 晴 高温 -1℃ 无持续风向 微风

字数有限

七年级数学正数和负数教案

滨州在山东北部.

滨州市是山东省下辖地级市，位于山东省北部、鲁北平原、黄河三角洲腹地，地处黄河三角洲高效生态经济区、山东半岛蓝色经济区和环渤海经济圈，是山东省的北大门；地势南高北低，大致上由西南向东北倾斜；辖四县二区一市,总面积9453平方千米。2018年总人口392.25万。

扩展资料：

截至2019年1月，山东省共辖16个地级市，分别是济南市、青岛市、淄博市、枣庄市、东营市、烟台市、潍坊市、济宁市、泰安市、威海市、日照市、滨州市、德州市、聊城市、临沂市、菏泽市。

滨州市位于山东省北部、黄河三角洲腹地、渤海湾西南岸，北通大海、东临东营市、南连淄博市、西南与济南市交界、西与德州市接壤、西北隔漳卫新河与河北省海兴县、黄骅市相望。

百度百科——滨州

为什么天老是闷热还不下雨，但天气预报的有雨啊？

　《正数与负数》这一模块的主要知识点是认识下数和负数，知道在什么情况下用正数和负数来表示。接下来是我为大家整理的 七年级数学 正数和负数教案，希望大家喜欢!

七年级数学正数和负数教案一

　教案背景

　初中生爱玩、好动，处于形象思维向 抽象思维 过渡的阶段，过分抽象的问题，学生往往感到乏味而百思不得其解。而多媒体具有形象、直观的特点，利用它为学生构建思维想象的平台，营造良好的学习氛围，充分调动学生学习的积极性、自觉性，用以达到以快乐的形式去追求知识的目的;新课程标准要求：课堂教学要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动，内容的呈现应用不同的表达方式，以满足多样化的学习需求。教学过程中。要加强学生的动手实践、自主探索与合作交流的意识，并着力培养学生解决实际问题的能力。

　1.1《正数和负数》教学设计方案

　(第1课时)

　人教版 九年级数学 上册

　山东省滨州市滨城区滨北街道办事处北城中学 耿新华

　邮编：256651 联系电话：15865403584

　教材分析：

　一、教材所处的地位及作用：“1.1正数和负数”一节，是人教版七年级上册第一章第一节的内容，本节内容主要是学习正数、负数和零的定义、联系。是本章有理数学习的基础。

　二、教学目标

　知识与技能：借助生活中的实例理解有理数的意义，会判断一个数是正数还是负数，能应用正负数表示生活中具有相反意义的量。

　过程与 方法 ：1.体会负数引入的必要性，感受有理数应用的广泛性，并领悟数学知识来源于生活，体会数学知识与现实世界的联系。

　2.能结合具体情境出现并提出数学问题，并解释结果的合理性。

　情感态度与价值观：乐于接触社会环境中的数学信息，愿意谈论数学话题，在数学活动中发挥积极作用。

　三、教学重、难点

　重点：体会负数引入的必要性和有理数应用的广泛性， 能应用正负数表示生活中的具有相反的意义的量。

　难点：能应用正负数表示生活中的具有相反的意义的量，养成把数学应用于生活实际问题的习惯。

　 教学方法 ：用“现象──问题──目标”的教学方法，力求体现“主体参与、自主探索、合作交流、指导引探”的教学理念

　教学过程

　教师在轻松欢快的音乐中演示第一节首为主体的多媒体课件。

　环节 教师活动 学生活动 设计意图

　创设情境导入新课

　自主学习

　师生互动

　合作探究

　达标检测

　 学习 总结

　教师出示说明自然数的产生、分数的产生.接着

　出示问题

　问题1 天气预报：滨州市冬季某天的温度为-3～3℃，它的确切含义是什么?这一天我市的温差是多少?

　问题2 2.2010年我国花生产量比去年增长1.8%油菜产量比去年增长-2.7%，这里的增长-2.7%代表什么意思?

　两个问题中的-3、-2.7%是我们以前没有学过的新数，这说明随着生活和劳动的发展我们以前学过的数，已经不够用了，需要引进新的数。来服务我们的生活。从而导入新课

　一、出示本节课的学习目标

　1、通过生活中实例认识到引入负数的必要性。

　2、知道什么是负数，零，正数。

　3、会判断一个数是正数?还是负数?

　4、能用正数、负数表示实际生活中具有相反意义的量

　二、出示本节课的自学提纲

　1、.知识点1：正数、负数的概念---------阅读教材第2页，像3、2、0.5、1.8%这样比0大的数叫 ，根据需要，有时在正数前面加上“+”，如+5， ， ， ，…。正数前面的“+”，一般省略不写：而像-3、-2、-3.5%这样在正数前面加上“—”号的数叫 。如-6， ，…。“-6”读作 。

　2、知识点2：对“0”的理解--------阅读教材第2 页

　0既不是 数，也不是 数，它是正数与负数的分水岭。它的意义很丰富，它既可以表示“没有”，也可以表示 其它 特定的意义。

　3、知识点3;用正数和负数表示具有相反意义的量--------阅读教材第3页

　相反意义的量必须具有两个要素：一是它们的意义 ;二是它们都具有数量，而且一定是 量。

　一、指导学生在本组内交流结果，收集每组不会的问题，试着让其他组解决。

　二、教师收集全班不会的问题，帮着解决。

　做一做：(出示幻灯片)

七年级数学正数和负数教案二

　1.1《正数和负数》教学设计方案

　(第1课时)

　教材分析：

　一、教材所处的地位及作用：“1.1正数和负数”一节，是人教版七年级上册第一章第一节的内容，本节内容主要是学习正数、负数和零的定义、联系。是本章有理数学习的基础。

　二、教学目标

　知识与技能：借助生活中的实例理解有理数的意义，会判断一个数是正数还是负数，能应用正负数表示生活中具有相反意义的量。

　过程与方法：1.体会负数引入的必要性，感受有理数应用的广泛性，并领悟数学知识来源于生活，体会数学知识与现实世界的联系。

　2.能结合具体情境出现并提出数学问题，并解释结果的合理性。

　情感态度与价值观：乐于接触社会环境中的数学信息，愿意谈论数学话题，在数学活动中发挥积极作用。

　三、教学重、难点

　重点：体会负数引入的必要性和有理数应用的广泛性， 能应用正负数表示生活中的具有相反的意义的量。

　难点：能应用正负数表示生活中的具有相反的意义的量，养成把数学应用于生活实际问题的习惯。

　教学方法：用“现象──问题──目标”的教学方法，力求体现“主体参与、自主探索、合作交流、指导引探”的教学理念

　教学过程

　教师演示第一节首为主体的多媒体课件。

　环节 教师活动 学生活动 设计意图

　创设情境导入新课

　自主学习

　师生互动

　合作探究

　达标检测

　学习总结

　教师出示说明自然数的产生、分数的产生.接着

　出示问题

　问题1 天气预报：北京市冬季某天的温度为-3～3℃，它的确切含义是什么?这一天我市的温差是多少?

　问题2 有三个队参加的 足球 比赛中，红队胜黄队(4：1)，黄队胜蓝队(1：0)，蓝队胜红队(1：0)，如何确定三个队的净胜球数与排名顺序?

　问题3 某机器零件的长度设计为100mm，加工图纸标注的尺寸为100 0.5(mm)，这里的 0.5代表什么意思?合格产品的长度范围是多少 ?

　三个问题中的-3、 0.5是我们以前没有学过的新数，这说明随着生活和劳动的发展我们以前学过的数，已经不够用了，需要引进新的数。来服务我们的生活。从而导入新课

　一、出示本节课的学习目标

　1、通过生活中实例认识到引入负数的必要性。

　2、知道什么是负数，零，正数。

　3、会判断一个数是正数?还是负数?

　4、能用正数、负数表示实际生活中具有相反意义的量

　二、出示本节课的自学提纲

　1、.知识点1：正数、负数的概念---------阅读教材第2页，像3、2、0.5、这样比0大的数叫 ，根据需要，有时在正数前面加上“+”，如+5， ， ， ，…。正数前面的“+”，一般省略不写：而像-3、-2、-0.5这样在正数前面加上“—”号的数叫 。如-6， ，…。“-6”读作 。

　2、知识点2：对“0”的理解--------阅读教材第2 页

　0既不是 数，也不是 数，它是正数与负数的分水岭。它的意义很丰富，它既可以表示“没有”，也可以表示其它特定的意义。

　3、知识点3;用正数和负数表示具有相反意义的量--------阅读教材第3页

　相反意义的量必须具有两个要素：一是它们的意义 ;二是它们都具有数量，而且一定是 量。

　一、指导学生在本组内交流结果，收集每组不会的问题，试着让其他组解决。

　二、教师收集全班不会的问题，帮着解决。

　做一做：(出示幻灯片)

　一个月内，小明体重增加2kg，小华体重减少1kg，小强体重无变化，写出他们这个月的体重增长值

　 七年级数学正数和负数教案三

　教学目标

　知识与技能：

　使学生了解正数与负数是从实际需要中产生的。

　过程与方法：

　在经历从具体例子引入负数的过程中，使学生理解正数与负数的概念，并会判断一个数是正数还是负数，初步会用正负数表示具有相反意义的量，理解0所表示的意义。

　情感与态度：

　在负数概念形成的过程中，培养学生的观察、归纳和概括能力，激发学生学好数学的热情。

　学情分析

　1.了解负数产生的背景(数的产生和发展离不开生活和生产的需要)，体会负数在生产和生活中运用的重要性。 2.学生经历负数引入的过程：生产和生活中的例子(具有互为相反意义的量)——数不够用——负数的引入——数学符号的表示——问题的解决等过程，初步培养学生数学符号感，了解数学符号在数学学习中的地位和作用。培养学生在与人合作交流的过程中，主动探究问题本质，善于观察、归纳、概括以及发现解决问题的方法的能力。

　重点难点

　正确认识正数和负数，理解0所表示的量的意义。

　教学过程

　教学活动

　活动1导入导入

　复习回顾，做好衔接 同学们已经有了六年学习数学的 经验 ，数对每一位同学来说并不陌生，相信同学们已经认识到数的产生和发展离不开生产和生活的需要。首先让我们来回顾： 自然数的产生、分数的产生。 演示课件，展示，直观说明数的产生和扩充：(出示说明自然数的产生、分数的产生。让学生理解数的符号的产生的好处) 师生活动(引导学生观察，试着解释意义)：我们知道，为了表示物体的个数(如原始社会打猎计数)或事物的顺序，产生了1，2，3，...;为了表示“没有”(比如猎物分完)，引入了数0;有时分配、测量(丈量土地)的结果不是整数，需要用分数(小数)表示. 总之，数是为了满足生产和生活的需要而产生发展起来的.

　设计意图：数的产生和发展离不开生活和生产的需要。

　活动2导入活动2

　演示课件，展示问题及相应的。

　问题(1)北京冬季里某天的温度为-3~3 ，它的确切含义是什么?这一天北京的温差是多少?

　问题(2)有三个队参加的足球比赛中，红队胜黄队(4：1)，黄队胜蓝队(1：0)，蓝队胜红队(1：0)三个队的净胜球数分别是2，-2，0，如何确定排名顺序?

　问题(3)2006年我国花生产量比上年增长1.8%，油菜籽产量比上年增长-2.7%，这里增长-2.7%代表什么意思?

　师生活动：教师演示课件并对问题背景做些说明：

　例如在净胜球的问题中，先介绍确定足球比赛排名顺序的规定：

　两队积分不相同，积分高的队排名在前;

　两队积分相同，净胜球多的队排名在前;

　两队积分、净胜球都相同，进球多的队排名在前。

　其次介绍积分计算规则：胜一场得3分，平一场得1分，输一场得0分。由此易知这三个队的积分均为3+0=3。

　最后介绍净胜球的计算规则：红队胜黄队(4：1)表示红队进4球，失1球或者黄队进1球，失4球，净胜球就是比赛中多进了几个球。这里进球和失球是互为相反意义的量。我们规定：进球用“+”，失球用“-”表示，这样进球数和失球数可分别在进球数和失球数前面添上“+”或“-”来表示。净胜球就是在比赛中进球与失球之和。比如以红队为例，进球为4，失球为2(两场比赛各失一球)记为-2，所以红队净胜球为4+(-2)=2.类似地可算出黄队净胜球-2(进球比失球少2个球，相当于净失球2个，所以记为-2)，蓝队净胜球是0.

　在教师的指导下，学生思考-3 ~3 、净胜球与排名的顺序、增长-2.7%的意义以及在解决这些问题时必须要对这些新数进行四则运算等问题。

　设计意图：通过温度的例子——出现新数-3还涉及到有理数的减法;净胜球的例子，也出现了负数，确定净胜球涉及有理数的加法，确定排名顺序涉及有理数的大小的比较;在产量增长率的例子中，运用正负数描述朝指定方向变化的情况等问题，引出用各种符号表示数，让学生试着解释，激发他们的求知欲，同时对问题进行说明，找出它们的共性，揭示问题的实质(具有相反意义的量)。

　具有相反意义的量的表示

　师生活动：鉴于上面的分析讨论，在教师的引导下，让学生试着归纳具有相反意义的量的表示：

　比如温度的问题，零上与零下(是以零为分界点)是具有相反意义的量，我们规定零上为正，则零下为负;净胜球的例子，进球与失球(对方进球)也是具有相反意义的量，我们规定进球为正，则失球为负…… 一般地，对于具有相反意义的量，我们可以把其中一种意义的量规定为正，并在其前面写上一个“+”(读作“正”)来表示;把与它意义相反的量规定为负的，并在其前面写上一个“-”(读作“负”)来表示(零除外)

　设计意图：由实例归纳具有相反意义的量的表示方法，培养学生合作交流意识及从特殊到一般认识问题本质的能力。

　 七年级数学正数和负数教案四

　〔教学目标〕

　一、知识与能力

　借助生活中的实例会判断一个数是正数还是负数，能用正负数表示具有相反意义的量

　二、过程与方法

　1、过程：通过实例引入负数，从而指导学生会识别正负数及其表示法，能应用正负数表示具有相反意义的量。

　2、方法：讨论法、探究法、讲授法、观察法。

　三、情感、态度、价值观

　乐于接触社会环境中的数学信息，愿意谈论数学话题，在数学活动中发挥积极作用

　〔重点难点〕本课的重点是了解正数与负数是由实际需要产生的以及有理数包括哪些数。难点是学习负数的必要性及有理数的分类。关键是要能准确地举出具有相反意义的量的典型例子以及要明确有理数分类的标准。

　正、负数的引入，有各种不同的方法。教材是由学生熟知的两个实例：温度与海拔高度引入的。比0℃高5摄氏度记作5℃，比0℃低5摄氏度，记作-5℃;比海平面高8848米，记作8848米，比海平面低155米记作-155米。由这两个实例很自然地，把大于0的数叫做正数，把加“-”号的数叫做负数;0既不是正数也不是负数，是一个中性数，表示度量的“基准”。这样引入正、负数，不仅有利于学生正确使用正、负数表示具有相反意义的量，而且还将帮助学生理解有理数的大小性质。把负数理解为小于0的数。教材中，没有出现“具有相反意义的量”的概念。这是有意回避或淡化这个概念。目的是，从正、负数引入一开始就能较深刻的揭示正、负数和零的性质，帮助学生正确理解正、负数的概念。

　关于有理数的分类要明确的是：分类标准不同，分类结果也不同，分类结果应是不重不漏，即每一个数必须属于某一类，又不能同时属于不同的两类。

　教学建议

　这节课是在小学里学过的数的基础上，从表示具有相反意义的量引进负数的.从内容上讲，负数比非负数要抽象、难理解.因此在教学方法和教学语言的选择上，尽可能注意中小学的衔接，既不违反科学性，又符合可接受性原则。例如，在讲解有理数的概念时，让学生清楚地认识有理数与算术数的根本区别，有理数是由两部分组成：符号部分和数字部分(即算术数).这样，在理解算术数和负数的基础上，对有理数的概念的理解就简便多了.

　为了使学生掌握必要的数学思想和方法，在明确有理数的分类时，可以有意识地渗透分类讨论的思想方法，理解分类的标准、分类的结果，以及它们的相互联系。通过正数、负数都统一于有理数，可以将对立统一的辩证思想的逐步树立渗透到日常教学中。

　一、负数的引入

　我们知道，数产生于人们实际生产和生活的需要。[投影1～3：图1.1-1]人们由记数、排序，产生了数1，2，3……;为了表示“没有”、“空位”引进了数0;测量和分配有时不能得到整数的结果，为此产生了分数和小数。

　在生活、生产、科研中经常遇到数的表示与数的运算的问题。

　[投影]1.北京冬季里某天的温度为-3～3℃，它的确切含义是什么?这一天北京的温差是多少?

七年级数学正数和负数教案相关 文章 ：

1. 初一上册数学《正数和负数》教案优秀范文五篇

2. 初一数学正数和负数教学

3. 七年级数学学习:正数和负数

4. 七年级数学上册教案

5. 七年级数学上教学设计2017

6. 七年级数学教案沪科

7. 初一数学教程:正数和负数

8. 七年级数学上册第1、2章教案

9. 人教版六年级下册《负数》教案范文5篇

10. 北师大初中七年级上册数学教案

为什么天老是闷热还不下雨，但天气预报的有雨啊？

天气预报不一定准，等一段可能就下了

为什么还不下雨啊 天气预报

天气预测的大概过程是这样的：从各处的气象站、观测点得到相关的各种资料，然后把这些引数放入气象学家设计好的数学模型中，通过计算机计算出预测结果。这个计算量是相当庞大的，因此在计算机出现以前完全不可能做到。所以预测准确与否很大程度取决于数学模型。

混沌理论则认为类似天气这样的东西是无法被预测的，（参看“蝴蝶效应”。）因此花费在气象预测上的钱也是浪费。

但是通过卫星云图预测某一地区近期的天气状况还是准确的，只是当预测到某个地方某个时刻的具体天气或者温度则有很大出入。

为什么天气预报会如此不准？中国气象局中央气象台的杨贵明高阶工程师解释道：“天气预报的准确率，是由观测资料的疏密决定。而我国现在的探空观测站一共只有100多个，折合每200多公里才有一个探空观测站。云的生命很短，一块大的雨云可能会在10公里内将雨降完，而雨没有降在观测点上，就观测不到。不仅探空站在空间上稀疏，在时间上也是如此，每天只有早8点和晚7点两次升起探空气球进行观测，其他时间仅靠地面观测站进行观测。而探空气球升起时没有遇到云，就无法预报。”

“几个小时发生的事情，在几天前就预报出来是不可能的。”杨贵明强调，“观测站就像是一张网中的点，网路越大、点越少则点与点之间的空隙也就越大，出现漏报、误报的机率也就越高。我国地域辽阔而天气观测的资金有限，所以出现漏报、误报也就在所难免。”

天气预报：先是有备，继而无患

天气预报只是一个概率预报，以降水为例，观测到冷空气入侵即将降下暴雨，这次降水的过程是可以准确预报的，然而具体到这场雨将会降落到哪个地区就只能提供一个概率了。可能北京是80%下，天津是50%。杨贵明介绍道：“目前小雨量降水落区的预报准确率在50%左右，最高能达到80%而最低只有30%多。大雨量降水落区的准确率只有30%左右。但是相比较上世纪只有百分之十几的准确率已经有了长足的进步。”

“大自然的想象是不受人控制的，人类只能摸索和利用。”杨贵明对记者说，“只有了解天气预报才能正确使用天气预报。就好像地震预警一样，即使报不准也得相信并取预防措施。天气预报也是如此，只是让你有备，才可能会无患。”

专家解析：准确率总在大幅度提高

到2010年，我国将初步建立气象综合观测系统，基本形成面向行业和全社会的气象资讯共享平台，大幅提高天气预报的准确率。

中国气象局局长秦大河院士在接受新华社记者访时表示，“十一五”期间，我国还将加强突发公共现场大气综合探测、无线资讯传输、应急气象资讯处理平台、视讯监控等应急系统装置建设；释出预报天数为7天的公众气象预报，台风、暴雨等气象预报质量提高5%至10%，24小时台风路径预报偏差在120公里内，年季旱涝、冷暖气候预测水平提高5%，粮食产量预报精度达95%以上，释出大气成分、雷电灾害、空间天气预报警报。建立重大灾害气象应急响应体系，提前半小时以上释出雷雨大风、山洪、泥石流等局地突发性灾害警报，气象预报警报公众覆盖率达95%。

究竟准不准，比比看

其实人们对于天气预报的不良印象还有个心理学的原因：出于思维的特点，人们总是会牢牢记住给他们造成不愉快经历的过程，而忽略带来愉悦的过程，这就是记忆的选择性。

为什么QQ上的天气预报报的有雨，咋就不下雨呢~？

那是因为什么都有失算德时候`没有万无一失德事情 笨笨，懂！

满意请纳

滨州为什么今天不下雨啊？天气预报说今天下雨啊？

呵呵 天气预报 也会有不准的时候啊~我也是滨州的

为什么天气预报天天预报有雨，就是不下雨，天气预报每时每秒都在更新吗？

天气预报也不能做到百分百准确，因为天气是随时都在变的，监测资料是有滞后性的。不是每时每秒在更新的。

为什么现在的天气预报老是报不准啊？说下雨不下雨，说晴天又下雨。

人家故意不报准的，报准了明年没有更多的经费～然后你懂的～

怎么不下雨啊天气预报不好使

看云：民间气象谚语说“鱼鳞天，不雨也风颠”、“乌云遮太阳不过三后晌”观霞：朝霞不出门，晚霞行千里。看动物：蜻蜓燕子低飞，蚂蚁搬家，鱼儿水面来换气儿，大雨马上就来到。蜻蜓千百绕，不日雨来到。蜜蜂花忙，短期有雨降。听风：半夜东风起

为什么今天不下雨，天气预报说下雨

这种情况很是正常，有如下原因：

1、天气预报不代表就是准确的天气实际情况，毕竟预报不是事实；

2、没有雨也不一定就是坏事，关键要根据天气情况调节个人心情，天气好就表示您会有好心情，何乐不为？

3、祝你快乐。

为什么，今天天气预报说不下雨，却下雨了

我这里天气预报就没准过。明明正在下雨，预报上说是阴天。小城市的不准，大城市，重要城市的可能准一些

兰考天气预报有雨为什么老不下

天气预报是根据一定原理来推测天气变化，但有一定程度上因为多种原因，使得天气多变，造成天气预报不准。例如：

蝴蝶效应 1960年，美国麻省理工学院教授洛伦兹研究“长期天气预报”问题时，在计算机上用一组简化模型模拟天气的演变。他原本的意图是利用计算机的高速运算来提高天气预报的准确性。但是，事与愿违，多次计算表明，初始条件的极微小差异，均会导致计算结果的很大不同。洛伦兹用一种形象的比喻来表达他的这个发现：一只小小的蝴蝶在巴西上空煽动翅膀，可能在一个月后的美国得克萨斯州会引起一场风暴——这就是混沌学中著名的“蝴蝶效应”，小朋友们大概都听说过吧，而根据这一理论，天气预报是不可能做到100%准确的。

数值天气预报 现在的大多数天气预报，可不再是“看云识天气”，而是有强大的计算机和很复杂的数学模型做后盾的。数值天气预报把大气的演变规律近似表示为一组数学方程式，根据从有限观测中得到的当前大气的初始状态，通过求解这一组方程式的解，得到对未来的天气或气候状况的预报。这可不是在数学课上学的方程哟，这方程的复杂程度，要用每秒执行数千亿次的超级计算机一刻不停地进行运算，才能求出近似解——你注意到了吗，“近似”这个词出现了两次，也就是说，无论是方程式，还是最终的解，都并不完美，所以有时在最终结果上有一些误差，也是难免的啦！

小范围突发极端天气 小朋友们有没有发现，现在的天气预报，对于像台风来袭、冷空气南下这样大范围天气影响的预报还是很准的，这可都是天上的气象卫星的功劳，气象卫星每天发回的卫星云图，帮助预测大范围天气的走势，但是气象卫星的观察范围至少也有一个省那么大，并且担负著观测全国天气的任务，不可能一直盯着一个城市看，于是那些在小范围内发生的突发极端天气，比如雷阵雨、雷暴、冰雹、龙卷风，卫星可就无能为力啦——这也是这些小范围突发极端天气难以预报的重要原因。